The 2D Julia fractal to the left is a shape that everyone recognizes. The simple formula that defines the Julia and Mandelbrot set is also something that many know:
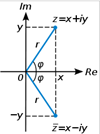
The variable z and constant c are in a normal 2D Julia set complex numbers. A complex number is a tuple of two values, a real and imaginary part, which can be visualized in the complex pane, which is a 2D geometric representation of complex numbers.
Complex numbers can be extended to a four-tuple value with one real and three imaginary units. These are called Quaternions and can be visualized as a four dimensional space. When using the Julia equation with Quaternions we can define a 4D dimensional object. It becomes a lot trickier to visualize however. What is needed is a 4D camera from which you can cast rays (vectors). The algorithm traverse these vectors step by step (from the camera) and for each point the Julia equation is recursively run to determine if the point is part of the Julia set or not.
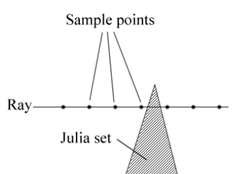
Here is 2D illustration of how a ray is thrown and sampled at regular intervals:
The process of sampling each point can be very time consuming so the distance between sample points can not be to small, but it can not be the to high either as it directly relates to the point resolution you get as exemplified by these two images:
The left image has a higher distance between sample points compared to the image to the right. You can clearly see the artifact of how the algorithm works in the rings in the image to the left (each ring is a sample point along the ray). To optimise the sampling process we can move back after a sample hit and then move forward in smaller steps.
Here is the Julia set viewed from the side, the constant (Julia seed) is (0.4 0.5i 0j 0k).
The raytracing gives coordinates in a 4D space that belongs to the Julia set, each point can be given a color depending on how far the point is from the camera (as above). Further each point can be lighted and shaded. To accurately light a point you need it's surface normal, these normals can be calculated by looking at the relative heights of neighbouring points (pixels).
The most fascinating aspect of 4D Julia sets can be viewed when you animated them. To animate them you render pictures with small change to the Julia seed constant or to the camera position. What is particularly interesting is when you move the camera in the fourth dimension. What you get is an animation of how the Julia set looks like from different four dimensional angles. It is hard to describe what happens, but basically the shape morphs into different shapes when viewed from different four dimensional angles :)
During the process of coding our raytracer we accidentally made an error in the quaternion multiplication, which resulted in a very strange shape:
We named these über quaternions. Later when we were writing the paper we discovered that we had used commutative multiplication rules which resulted in hypercomplex numbers.
Here is another picture showing how the shape gets more detail depending on the number of times you recurse over the Julia algorithm:
Isn't it fascinating and beautiful how such a simple algorithm can define such an intricate structure? The raytracer was witten in C++ and my plan is to (someday, maybe next year) port / rewrite it in F# :)
The paper is very technical so I doubt that it will interest many, but here is the link and abstract:
By using rules defined by quaternion algebra the Julia set can be extended to four dimensions. Techniques for visualizing the four dimensional Julia set as a three dimensional object has previously been explored, however those techniques usually ignores the fourth dimension. In this paper we describe our attempt to extend the already established technique of ray tracing Julia sets to fully incorporate its four dimensional properties. We also discuss an optimisation algorithm that drastically increases the amount of details in images and shortens rendering time.
Link to the paper: Raytracing4D.pdf
Movies:
- 4D Camera move: 4d_cameramove.avi
- Another 4D Camera move: r4d.avi
- Moving the seed in circle (on the complex pane): cycle.avi
- Moving the seed from left to right (on the complex pane): cwalk.avi
- Moving the camera in a circle around the hypercomplex julia set: uber_highres.avi
It is worth pointing our that in the two first movies with 4D camera movies it is only the camera that is moving the julia seed never changes, only the angle that the object is viewed at. The paper was written with LaTeX, which was a lot of fun to learn, although quite hard to use. But the output looks so much more professional.
Were you also a graphics geek? Did you write a flame or plasma effect in assembler, did you use allegro to write DOS games? I sure did :)